Natural Frequency of a Spring-Mass System
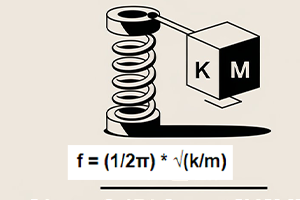
Natural Frequency of a Spring-Mass System
Where:
Practical Uses of Natural Frequency Formula:
- Automotive Suspension Systems: Understanding the natural frequency helps in designing suspension systems that provide optimal comfort and stability for vehicles.
- Building Design and Seismic Analysis: Architects use natural frequency calculations to ensure buildings can withstand seismic forces without collapsing or suffering significant damage.
- Medical Devices: In medical devices like pacemakers, understanding natural frequencies is crucial for ensuring proper functioning and avoiding harmful resonance.
- Aerospace Engineering: Natural frequency analysis is essential in aerospace engineering to predict how structures will respond to various loads and vibrations during flight.
- Consumer Electronics: Designers of consumer electronics, such as smartphones and laptops, use natural frequency calculations to minimize vibration-induced noise and improve product durability.
Frequently Asked Questions (FAQs)
1. What is the natural frequency of a spring-mass system?
The natural frequency is the frequency at which the system oscillates when it is not subjected to any external forces.
2. How do I calculate the natural frequency?
The natural frequency can be calculated using the formula: \( f_n = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \).
3. What are the units for spring constant and mass in this formula?
The spring constant \( k \) is measured in N/m and the mass \( m \) is measured in kg.
4. Why is natural frequency important in engineering?
Natural frequency helps engineers design systems that can withstand various loads and vibrations without failing or causing damage.
5. Can natural frequency be applied to real-world scenarios like car suspension systems?
Yes, natural frequency is crucial in designing car suspension systems to ensure smooth ride quality and stability.
6. How does natural frequency affect building design during seismic analysis?
Understanding natural frequency helps architects ensure buildings can resist seismic forces without collapsing or suffering significant damage.
7. Is natural frequency relevant in medical devices like pacemakers?
Yes, it is essential for ensuring proper functioning of medical devices by avoiding harmful resonance frequencies.
8. What role does natural frequency play in aerospace engineering?
Natural frequency analysis predicts how structures will respond to various loads and vibrations during flight, ensuring safety and performance.
9. How does natural frequency impact consumer electronics design?
Designers use natural frequency calculations to minimize vibration-induced noise and improve product durability in consumer electronics like smartphones.
10. Can I use this formula for any type of spring or mass?
This formula applies specifically to idealized spring-mass systems; real-world applications may require additional considerations.
11. What happens if the natural frequency matches an external force frequency?
If the natural frequency matches an external force frequency, it can lead to resonance, which may cause significant amplification of motion or even failure.
12. How do I measure the spring constant \( k \) in practice?
The spring constant can be measured by applying known forces and measuring the resulting displacements using Hooke's Law: \( F = kx \).
13. Can I use this formula for systems with multiple springs or masses?
The formula provided is for a single spring-mass system; more complex systems require more advanced analysis techniques.
14. Are there any assumptions made when using this formula?
Yes, this formula assumes an idealized spring-mass system with no damping or frictional forces present
15. How can I ensure that my system does not resonate at its natural frequency?
To avoid resonance, you can design the system so that its natural frequency does not match any of the frequencies of external forces it may encounter. This can be achieved by adjusting the spring constant or mass, or by introducing damping mechanisms to reduce the amplitude of oscillations.

 Pneumatic-Hydraulic
Pneumatic-Hydraulic  Materials-Weight
Materials-Weight
 Miscellaneous Cal's
Miscellaneous Cal's Mechanics
Mechanics